古墳時代の数学 数学への興味関心を 高める
富田学園 岐阜東高校 亀井喜久男
古代日本 数学奥義 Mathematics in the Ancient Japan
古代メソポタミアから古代中国を経由して伝えられ古墳時代の日本(倭、邪馬台国)で独自の発展を加えた数学、数学的技術の話
これまで日本の数学は 6世紀(欽明天皇期)に百済から暦博士固徳王保孫が来日したこと、7世紀(推古天皇期)に設立された 陰陽寮にて陰陽、天文、暦、漏刻等の博士がいて中国からの輸入の陰陽道、天文 暦法などを研究していたことが日本書紀に伝えられている。いま流行の陰陽師である。 このころすでに九九は広がっていたとされている。 日本数学史は現在ここまでが調べられているが、私は漢から伝えられた方格規矩四神鏡のデザインと文字の解釈によって、日本数学史は百済の博士の数学書を携えての来日以前に遡ることが可能となると判断するにいたった。縄文以来の日本の数学文化は大陸(漢)からの文化に触発を受け、古墳造営とともに日本数学史は始まるのである。巨大土木工事である大山古墳(仁徳陵)などの築造に関する数学である。これだけ大規模な工事が幾何学なしでできるわけがなく、どのような数学がどう関わっていたかが重要であるが その形が見えてきたのである。 これから紹介する幾何学的知恵の源流は古代バビロニアにある。これは太古エジプトに伝えられピラミッド建造に役立ったと考えられている。後に戦国時代の中国に伝わり天文、時刻制度、政治制度などに影響を与えている。その後、漢の時代に方格規矩鏡(漢代に作られ霊力を持つと信じられた銅鏡)とともに日本にやってきたのである。12支の知識も同じように古代バビロニアに起源をもつと考えられている。輸入されたあとに この知恵は独自の発達を日本で遂げていくのである。大陸の12等分の輪状のひも 、わが国の24等分の輪状のひも これらをどちらも紹介したい。今も昔も技術の受け入れは真似だけではなく必ず発展を引き起こすことが日本の強みである。古代は独自の巨大前方後円墳へつながった。さらに技術は日本中に急速に広がった。古代、数学は輝いていた。しかし天文、暦、占いなどが国家の重大事項ということで秘密事項となり技術はおそらく一子相伝などによってのみ伝わることとなった。そして歴史のなかで消えていったのである。しかし隠されていた古代の秘密がいま甦る.

大陸のアイデア
12等分した輪になった縄紐(通称エジプトひも)
参考文献 実験数学のすすめ 銀林浩編 国土社 亀井喜久男 エジプトひもで古代文明に挑戦しよう古代文明、幾何学の源流に学ぶ
中国神秘数字 葉ジョ憲 田大憲 青土社
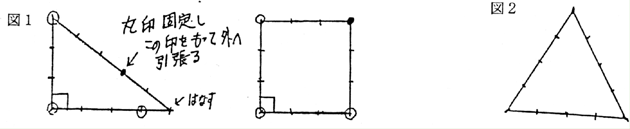
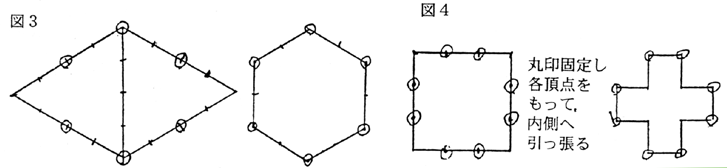
この道具が以下のように使われていただろうと推定したのは亀井に依っている。 12等分したひもの等分する点を結び目、または印と呼ぶ。3ヶ所の結び目を持ってピンと引張ることで、さまざまな 幾何学図形ができる。正方形、正三角形、正六角形、十字形などである。また自然界の性質を利用することで方角や日時計、天体観測装置なども作ることができる。
東西南北の決定
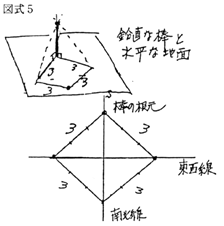
棒を地面に垂直に立てる。影の長さが3単位になるときが、午前と午後に1度ずつある。午前の影の先端と棒の正確な根元と午後の影の先端とあと1点に結び目を当てて一辺3単位のひし形を作る。このひし形の対角線が東西線 南北線である。棒を含むほうが南北線となる。
12方位の決定
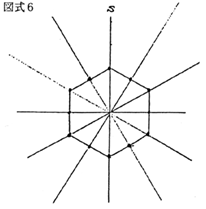
4,4,4の辺の長さを持つ正三角形を1辺を南北線に沿わせるように張って固定する。各辺の中点をくいで記録する。さらに南北線を線対称の軸にして反対側でも正三角形を作図しやはり中点をくいで記録する。はじめの正三角形の南北線上の2頂点と南北線上にない4つの中点は正六角形をなす、紐をこの六点に印をあわせて張りなおせばこの図形の中心(南北線の中点)からみると12個の印は12の方位を示していることになる。
日時計の製作
平面の板に正六角形を定規コンパスで描き、この平板を行動面と平行に置くことする この中心にくいを立ててそのなす影を見ていけば影は経過時間に比例して、12個の印のうち南側の印を指し示しながら回転していく。これすなわち日時計である。
夜には太陽の通り道(黄道)の星座の動きの観測をすれば時計になる。黄道12宮は 夜間の時計であるのみならず、木星が1年に1宮を通過することで1年の確認ができるようになる。これは実は年齢や歴史の始まりと言ってよい。
碁盤の目の形に田のあぜ道を引く
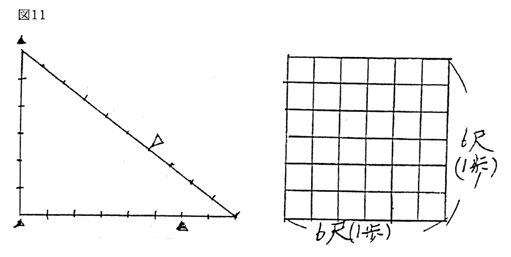
南北線に3の長さの一辺をあわせることとして3:4:5となるように直角三角形をひくこれで実は正方形の半分ができている。 そのあと3点を固定しある1点を持ってピンと引っ張れば1辺3の正方形ができあがりである。
古代日本のアイデア
24等分された輪になったひも 印から印までを1単位とする。
1単位1尺とすると 辺長6尺 周長 4歩 古代の面積単位 1歩(現在の1坪、長さと同じ字)
1単位を10歩で 辺長60歩 周の長さを240歩とすると 古代の条里制の 一区画(1町)
1単位を1町とすると辺長6町 周長 24町 古代の条里制の 1条里(本来の1坪)
日本では6が重視されている。
参考文献 古代の土木設計 椚 国男 六興出版
古鏡 小林行雄 学生社
前方後円墳 上田宏範 学生社
図解 単位の歴史辞典 小泉袈裟勝 編著
この24等分ひもでは何ができるだろうか。大陸でできたことはすべてできる。12等分の印はもちろん持っているからである 。それを業とする人々を方士と大陸では呼んでいた。日本にきたといわれる除福も方士であったと言われている。 大きく2通りの利用法が考えられる。 8かける8の 方格をある方法で作ってしまう。 また6かける6の方格もあっさりと作ってしまうのである。8は日本人が古くから大好きな数で、その8の倍数であるからこそ24等分のひもが考え出され始めたと推定している。
8:4:8:4
の長方形をまず作図する。8の辺をはじめに決めた方向に、8の辺の中点をはじめに定めた中心点に置く。この長方形によって方眼の線を引くことができる。中心軸と対称にもうひとつ長方形を作図する。
図式A
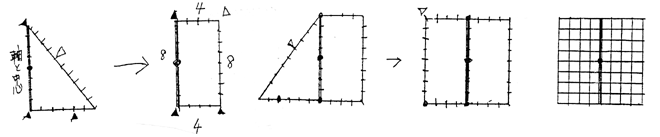
この方格によって古墳は設計されると推定したのが椚国男氏である。
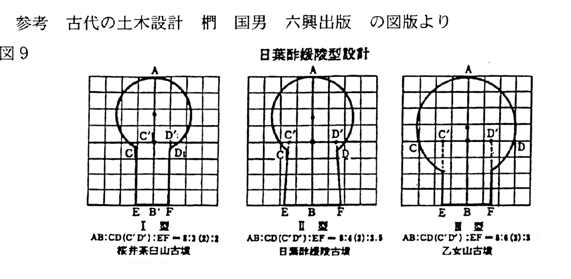
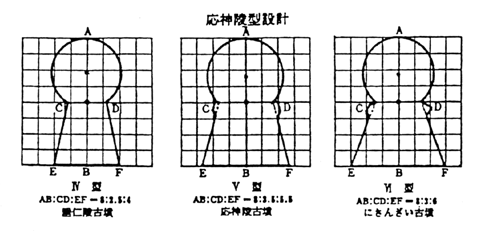
また方格地割がなされていると豊富な実例を上田宏範氏が紹介されている。古墳の兆域は方格地割の設計がなされているし都市設計 地図製作にも当然方格地割は活躍している。
次に6:8:10の直角三角形から 1辺6の正方形が作られる。6かける6の正方形は日本古代の地割の基本である。
6尺が1歩 約1.8m 60歩で1町 6町で 1短里 6短里で1長里 この長さは 古代条里制の遺構にも見られる。
面積の単位は1歩四方で1歩(今の一坪) 1町四方で 3600歩 1町 これを10反
古代日本における応用の代表例はこの2つである。かくのごとく大陸とは異なる縄の利用が考えられるのである。それを我々は古墳の形や 距離の名称の制度に 名残として見ることができるのである。
古代日本の数学に関するなぞはいくらでもある。慎重に証拠を探しながらなぞに挑戦しよう。それはこの小論に動かされるところのあった読者の仕事である。大陸での縄の使い方も日本での縄張りの方法も完璧な検証を経ているわけではない。たとえば中国古代に井田法はなかったとの論調が強い。歴史地理学者が井田法そのものの遺構をさぐりあてているにも関わらずである。証拠といえそうな資料の所在はできれば亀井に伝えていただきたいまとめて多くの方に伝えたいと思っている。この依頼をもって この論文を締めくくりたい。なおこの研究はこれからのアジアの初等数学教育の礎石となりたいとの希望をもって書かれたことを付記させていただく。多くの協力者の方々に謝意を伝えたい。
感想は右記へ kamei-ki@ma.ctk.ne.jp
 岐阜県琴塚古墳航空写真
岐阜県琴塚古墳航空写真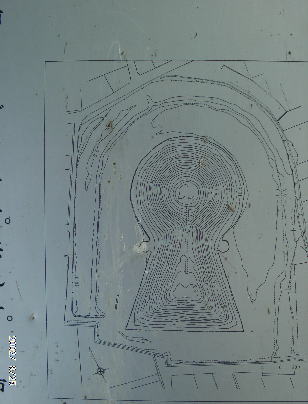 琴塚古墳調査図
琴塚古墳調査図
 琴塚古墳近景
琴塚古墳近景
実は鷺(サギ)のコロニーになっている。
 各務原市坊の塚古墳近景
各務原市坊の塚古墳近景
 各務原市坊の塚古墳航空写真
各務原市坊の塚古墳航空写真
 可児市長塚古墳近景
可児市長塚古墳近景
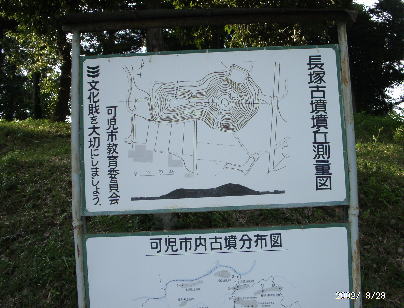 長塚古墳測量図
長塚古墳測量図
index









 岐阜県琴塚古墳航空写真
岐阜県琴塚古墳航空写真 琴塚古墳調査図
琴塚古墳調査図 琴塚古墳近景
琴塚古墳近景 各務原市坊の塚古墳近景
各務原市坊の塚古墳近景 各務原市坊の塚古墳航空写真
各務原市坊の塚古墳航空写真 可児市長塚古墳近景
可児市長塚古墳近景 長塚古墳測量図
長塚古墳測量図